算法的大O复杂度的说法

海龙2024-10-22编程JS/TS

这种东西，学的时候知道，然后就给忘了，不过写一次，就是回想和思考一次，也许就能真正思考到项目众如何使用起来。

首先，为什么要研究这个？

TIP

为了能让你开发的东西能做的更好

对于大多数情况来说，对于开发的程序或者软件来说，语言和框架，已经帮我们做到了很多优化，若非特殊需求，几乎是不需要将这些算法应用到开发中的。
常见的算法，也都会有前人写好的工具函数来直接使用。但是为了能从最基础的开发人员，向技术更深一步迈进，就需要去了解这些。

资源权衡,让你在时间和空间的角度，权衡并决策应当使用哪一种方式来执行你的程序。比如你要做一个嵌入式系统的应用，那么优化内存的使用是很关键的。
算法优化，根据你的项目某些计算的计算量，选择使用不同算法，如果计算量小，指数阶会表现更快，如果计算量大，那么换用对数阶算法也许是更好选择。

时间复杂度

所谓时间复杂度，是在说算法运行的时间随着数据越来越大，所需要运行的时间增长趋势。

设输入的数据量为n，那么常见的时间复杂度：
常数阶O(1) < 对数阶O(logn) < 线性阶O(n) < 线性对数阶O(nlogn) < 平方阶O(n²) < 指数阶O(2ⁿ) < 阶乘阶O(n!)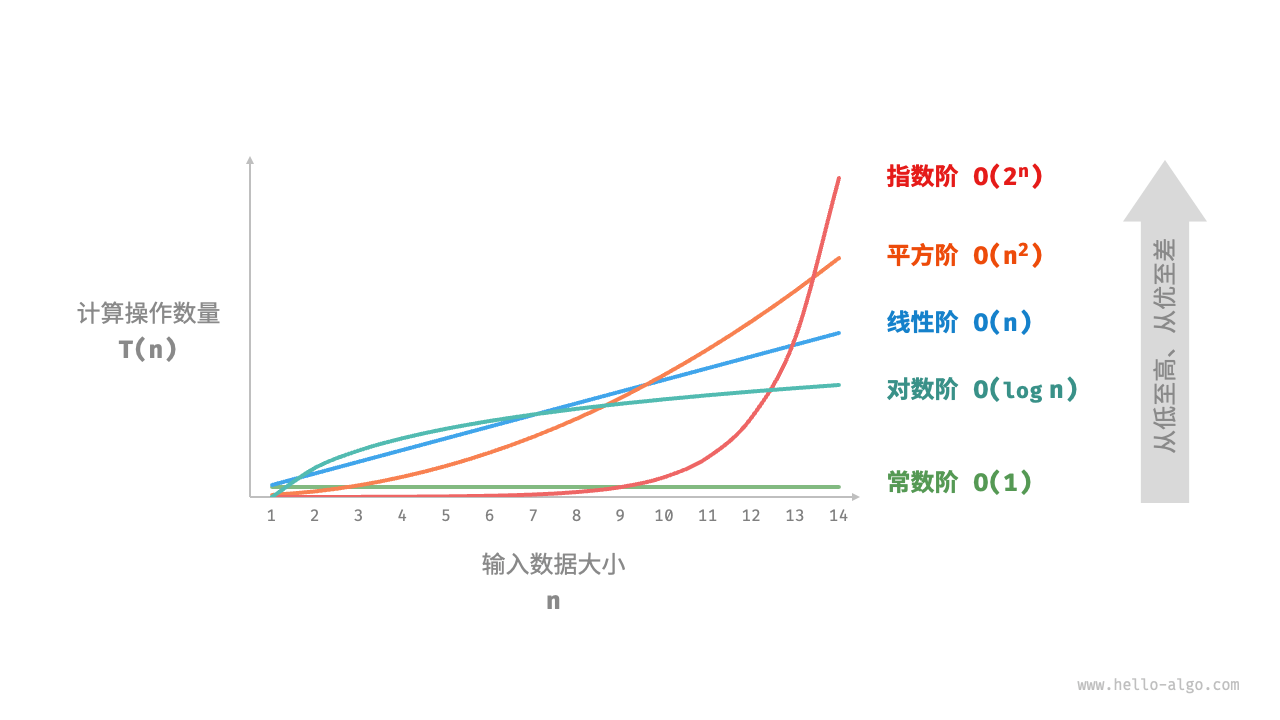

空间复杂度

空间复杂度表示算法在运行过程中额外占用的内存空间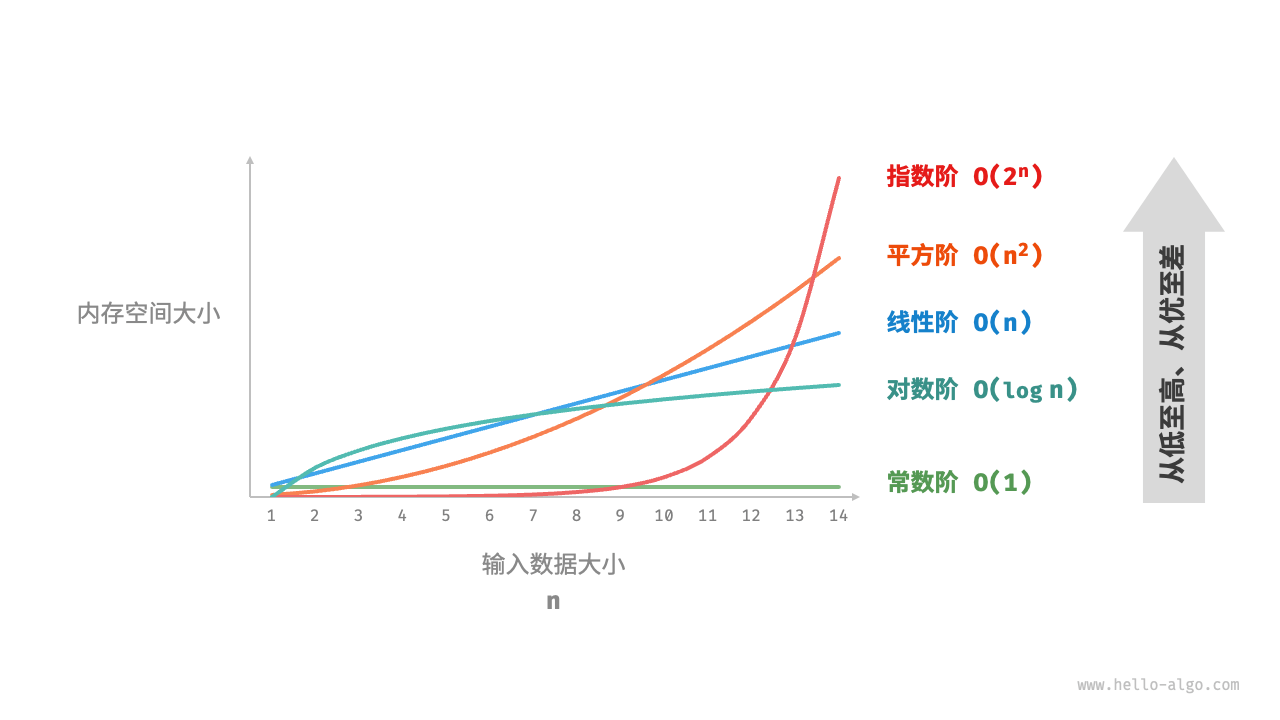

时间复杂度示例js代码

常数阶O(1)

常数时间复杂度表示算法的执行时间不会随着输入规模变化，它总是固定的。

function constantOperation(arr) {
  // 无论数组多大，只执行一次
  console.log(arr[0]); // 常数时间操作
}

对数阶O(logn)

对数时间复杂度通常出现在折半查找等场景，例如二分查找。

function logarithmicOperation(arr, target) {
  let left = 0;
  let right = arr.length - 1;

  while (left <= right) {
    const mid = Math.floor((left + right) / 2);

    if (arr[mid] === target) return mid; // 找到目标，退出
    else if (arr[mid] < target) left = mid + 1;
    else right = mid - 1;
  }

  return -1; // 未找到
}

线性阶O(n)

function linearOperation(arr) {
  for (let i = 0; i < arr.length; i++) {
    console.log(arr[i]); // 遍历数组，每次访问一个元素
  }
}

线性对数阶O(nlogn)

function mergeSort(arr) {
  if (arr.length <= 1) return arr;

  const mid = Math.floor(arr.length / 2);
  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));

  return merge(left, right);
}

function merge(left, right) {
  let result = [];
  let i = 0;
  let j = 0;

  while (i < left.length && j < right.length) {
    if (left[i] < right[j]) result.push(left[i++]);
    else result.push(right[j++]);
  }

  return result.concat(left.slice(i)).concat(right.slice(j));
}

平方阶O(n²)

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]; // 交换
      }
    }
  }
  return arr;
}

指数阶O(2ⁿ)

function fibonacci(n) {
  if (n <= 1) return n;
  return fibonacci(n - 1) + fibonacci(n - 2);
}

阶乘阶O(n!)

function permute(arr) {
  if (arr.length === 0) return [[]];

  let result = [];

  for (let i = 0; i < arr.length; i++) {
    const current = arr[i];
    const remaining = arr.slice(0, i).concat(arr.slice(i + 1));
    const remainingPermutations = permute(remaining);

    for (let permutation of remainingPermutations) {
      result.push([current].concat(permutation));
    }
  }

  return result;
}

空间复杂度示例js代码